[Paper]
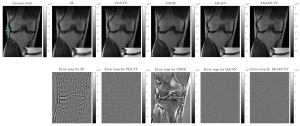
Medical image reconstruction is often an ill-posed inverse problem. In order to address such ill-posed inverse problems, prior knowledge of the sought after object property is usually incorporated by means of regularization. For example, sparsity-promoting regularization in a suitable transform domain is widely used to reconstruct images with diagnostic quality from noisy and/or incomplete medical data. However, sparsity-promoting regularization may not be able to comprehensively describe the actual prior information of the objects being imaged. Deep generative models, such as generative adversarial networks (GANs) have shown great promise in learning the underlying distribution of images. Prior distributions for images estimated using GANs have been employed as a means of regularization with impressive results in several linear inverse problems in computer vision that are also relevant to medical imaging. However, in practice, it can be difficult for a GAN to comprehensively describe prior distributions, which can potentially lead to a lack of fidelity between the reconstructed image and the observed data. Recently, an image-adaptive GAN-based reconstruction method (IAGAN) was proposed to guarantee stronger data consistency by adapting the trained generative model parameters to the observed measurements. In this work, for the first time, we apply the IAGAN method to reconstruct images from undersampled magnetic resonance imaging (MRI) measurements. A state-of-the-art GAN model called Progressive Growing of GANs (ProGAN) was trained on a large number of ground truth images from the NYU fastMRI dataset, and the learned generator was subsequently employed in the IAGAN framework to reconstruct high fidelity images from retrospectively undersampled experimental k-space data in the validation dataset. It is demonstrated that by use of the GAN-based reconstruction method with noisy and/or incomplete measurements, we can potentially recover fine structures in the object that are relevant for medical diagnosis that may be difficult to achieve using traditional reconstruction methods relying on sparsity-promoting penalties.
Publications
- Bhadra, S., Zhou, W. & Anastasio, M. A. (2020). In Medical Imaging 2020: Physics of Medical Imaging, vol. 11312, p. 113120V. International Society for Optics and Photonics, 2020.